Balistica esterna

La balistica esterna (termine usato la prima volta da Marin Mersenne nel 1644^[1] deriva dal greco βάλλειν, lanciare) è la scienza che studia il moto di un proietto dall'istante in cui termina la sua fase di accelerazione fino a quando colpisce il bersaglio. La balistica esterna è generalmente applicata alle armi da fuoco, e descrive il volo del proietto dalla bocca da fuoco fino al bersaglio, nel caso vengano utilizzati proietti non autopropulsi.

Storia

La balistica come scienza nasce con Galileo Galilei e la pubblicazione nel 1632 dei suoi studi che dimostravano come la traiettoria di un proietto nel vuoto, sottoposto all'attrazione gravitazionale, fosse una parabola.^[2] Galileo stesso si rese conto come trascurare la resistenza dell'aria portasse un errore nei calcoli balistici soprattutto per la furia soprannaturale dei tiri dei moschetti, mentre, a ragione, era trascurabile per i mortai dell'epoca.^[3] Le teorie di Galileo rimasero la base per i manuali d'artiglieria durante tutto il secolo XVII e XVIII, per esempio nel The complete gunnery del 1672 in lingua inglese che riportava le teorie balistiche di Galileo sviluppate da Evangelista Torricelli e ne Le bombardier français del 1730 di Bernard Forest de Bélidor.^[3] Molti scienziati cercarono di risolvere il contributo della resistenza dell'aria nel moto del proiettile, tra cui Newton e Bernoulli ma la non linearità delle equazioni differenziali ed alcuni parametri fondamentali che non erano stati misurati con sufficiente precisione (la velocità alla volata del proiettile e la resistenza dell'aria su di un proietto di forma nota) non permisero di ottenere risultati coerenti con le osservazioni.^[3] Con la pubblicazione, nel 1742, del New Principles of Gunnery di Benjamin Robins e la sua traduzione in tedesco, corredata da una ampia analisi matematica, da parte di Eulero la balistica esterna raggiunse una maturità tale da innescare, insieme ai progressi della metallurgia e della chimica degli esplosivi, un rapido sviluppo delle artiglierie definita rivoluzione balistica, parte della rivoluzione militare che portò all'ascesa delle potenze occidentali nel mondo.^[3] Robins con l'ideazione e l'impiego scientifico di due nuovi strumenti, il pendolo balistico, per la misurazione della velocità dei proietti ed il maneggio aerodinamico (uno strumento munito di due bracci orizzontali che messi in rotazione a velocità costante permetteva la misurazione della resistenza dell'aria esercitata su di un corpo fissato alle estremità dei bracci), pose le basi degli studi aerodinamici.^[3] Gli studi di Eulero e Robins permisero la creazione di tabelle di tiro, basate su soluzioni approssimate delle equazioni differenziali adeguate alla tipologia di arma, come quelle compilate dall'ufficiale tedesco Henning Friedrich nel 1764, che rimasero valide, per i mortai, fino agli inizi del novecento.^[3]

Balistica nel vuoto

Gittata di un proiettile con alzo θ, quota y₀ e gittata d

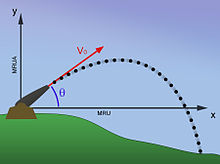
In questa ipotesi il proietto procede nel vuoto ed è soggetto alla sola forza di gravità, applicata al centro di gravità e costantemente verticale.

Il moto risulta uniformemente decelerato e la traiettoria è una parabola che interseca il piano di tiro nei due punti costituiti dalla posizione della bocca da fuoco e il punto d'impatto del proiettile. Si considerano le seguenti variabili:

g: forza peso o forza di gravità—approssimata a 9.81 m/s² alla superficie terrestre
θ: l'angolo di alzo (o elevazione) formato dall'asse del cannone con il piano orizzontale
v: velocità alla volata del cannone
y₀: quota iniziale del proietto
d: la gittata orizzontale, distanza totale percorsa dal proietto

Gittata orizzontale

La distanza totale percorsa dal proietto (d).

d={\frac {v\cos \theta }{g}}\left(v\sin \theta +{\sqrt {(v\sin \theta )^{2}+2gy_{0}}}\right)

Con una altezza iniziale del proietto pari a zero e considerando una superficie orizzontale, tra il cannone ed il bersaglio, la gittata sarà:

d={\frac {v^{2}\sin(2\theta )}{g}}

Si nota come la massima gittata si ottiene con θ pari a 45°gradi:

d={\frac {v^{2}}{g}}

Esistono due traiettorie equivalenti (una tesa ed una curva), nelle condizioni citate, per colpire un punto P se questo è posto ad una distanza inferiore alla massima gittata (d). Si ottengono sparando con angoli di proiezione simmetrici sfalsati di 45°+ $theta$ , come dimostrato da Galileo Galilei.

Durata del tragitto

La durata del tragitto (t) è il tempo impiegato dal proietto a completare la traiettoria.

t={\frac {d}{v\cos \theta }}={\frac {v\sin \theta +{\sqrt {(v\sin \theta )^{2}+2gy_{0}}}}{g}}

Considerando, come sopra, l'altezza iniziale pari a zero e la superficie orizzontale:

t={\frac {{\sqrt {2}}\cdot v}{g}}

se θ è 45° e y₀ è 0.

Angolo di alzo

L'"Angolo di alzo" è l'angolo (θ) che deve formare l'asse di tiro del proietto con l'orizzontale per poter raggiungere la distanza d, alla data velocità iniziale v.

\sin(2\theta )={\frac {gd}{v^{2}}}

\theta ={\frac {1}{2}}\arcsin \left({\frac {gd}{v^{2}}}\right)

Sviluppo per una gittata arbitraria `x`

Altezza raggiunta per `x`

L'altezza raggiunta dal proietto y alla distanza x è data da

y=y_{0}+x\tan \theta -{\frac {gx^{2}}{2(v\cos \theta )^{2}}}

.

Velocità del proietto alla distanza `x`

Lo scalare della velocità $|v|,$ alla distanza x è dato da

|v|={\sqrt {v^{2}-2gx\tan \theta +\left({\frac {gx}{v\cos \theta }}\right)^{2}}}

.

Derivazione

Lo scalare della velocità |v| può essere espresso anche come

|v|={\sqrt {V_{x}^{2}+V_{y}^{2}}}

,

dove V_x e V_y sono le velocità istantanee nelle direzioni x- e y-.

Qui la velocità-x rimane costante; è sempre uguale a v cos θ.

La velocità-y può essere trovato con la formula

v_{f}=v_{i}+at

considerando v_i = v sin θ, a = -g, e $t={\frac {x}{v\cos \theta }}$ . (quest'ultima si ottiene considerando x = (v cos θ) t e risolvendola per t.) così,

V_{y}=v\sin \theta -{\frac {gx}{v\cos \theta }}

e

|v|={\sqrt {(v\cos \theta )^{2}+\left(v\sin \theta -{\frac {gx}{v\cos \theta }}\right)^{2}}}

.

Alzo $\theta$ richiesto per colpire le coordinate (`x`,`y`)

Per colpire un bersaglio alla gittata x ed altitudine y sparando dall'origine (0,0) e con una velocità iniziale v l'angolo(i) di alzo $\theta$ sono:

\theta =\arctan {\left({\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}\right)}

Ogni radice dell'equazione rappresenta due possibili angoli di alzo a meno di soluzioni immaginarie, per cui la velocità iniziale non è sufficiente a raggiungere la gittata (x,y) richiesta.

Derivazione

Si propongono due formule base del moto di un proietto:

x=vt\cos \theta ,t={\frac {x}{v\cos \theta }}

(1)

y=vt\sin \theta -{\frac {1}{2}}gt^{2}

(2)

Risolvendo la (1) per t e sostituendola nella (2) si ha:

y=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}

(2a)

y=x\tan \theta -{\frac {gx^{2}\sec ^{2}\theta }{2v^{2}}}

(2b) (identità trigonometrica)

y=x\tan \theta -{\frac {gx^{2}}{2v^{2}}}(1+\tan ^{2}\theta )

(2c) (identità trigonometrica)

0={\frac {-gx^{2}}{2v^{2}}}\tan ^{2}\theta +x\tan \theta -{\frac {gx^{2}}{2v^{2}}}-y

(2d) (semplificazione)

Sia $p=\tan \theta$

0={\frac {-gx^{2}}{2v^{2}}}p^{2}+xp-{\frac {gx^{2}}{2v^{2}}}-y

(2e) (sostituzione)

p={\frac {-x\pm {\sqrt {x^{2}-4({\frac {-gx^{2}}{2v^{2}}})({\frac {-gx^{2}}{2v^{2}}}-y)}}}{2({\frac {-gx^{2}}{2v^{2}}})}}

(2f) (soluzione di Equazione di secondo grado)

p={\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}

(2f) (semplificazione)

\tan \theta ={\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}

(2g) (sostituzione)

\theta =\tan ^{-1}{\left({\frac {v^{2}\pm {\sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}\right)}

(2h) (semplificazione)

Balistica nell'aria

La resistenza dell'aria è direttamente proporzionale alla velocità del proiettile ( $F_{a}\propto {\vec {v}}$ ) fino a velocità subsoniche (basso numero di reynolds) per poi divenire proporzionale al quadrato della velocità una volta raggiunto un numero di Reynolds nel campo del regime turbolento. Questo avviene tra i 240 m/s e i 340 m/s, quest'ultima è la velocità del suono a 15 °C.^[4] Gli effetti sulla traiettoria rispetto al quella nel vuoto sono una gittata notevolmente diminuita, il punto più alto della traiettoria non è più a metà del tragitto ma viene raggiunto prima, l'angolo di caduta è maggiore di quello di alzo e la velocità terminale sul bersaglio è minore di quella iniziale.^[5]

Le equazioni del moto del centro di gravità del proietto all'interno di un fluido stazionario si possono rendere come:^[6]

m{\frac {dV_{x}}{dt}}=mV_{x}{\frac {dV_{x}}{dy}}=-{\frac {C_{d}\rho AVV_{x}}{2}}-mg

m{\frac {dV_{y}}{dt}}=mV_{y}{\frac {dV_{y}}{dy}}=-{\frac {C_{d}\rho AVV_{y}}{2}}

v^{2}=V_{x}^{2}+V_{y}^{2}

m massa del proietto, V_x e V_y le componenti della velocità V del proietto, C_d coefficiente di resistenza aerodinamica, ρ densità dell'aria, A area della sezione frontale del proietto e g è l'accelerazione di gravità.

Caso di un proietto non stabilizzato

Il passaggio dai proietti sferici dei cannoni del XVIII secolo alla forma affusolata ed ogivale dei proietti moderni ha comportato la soluzione del problema della stabilizzazione dei proiettili. Il centro di gravità di un proietto ogivale è posteriore rispetto al centro di applicazione della risultante delle forze che agiscono sul proietto in volo.^[7] Per effetto della forza di gravità la traiettoria si abbassa mentre il proietto tende a mantenere lo stesso orientamento per inerzia.^[8]

Il centro di gravità ed il centro di applicazione delle forze aerodinamiche non giacciono più sulla tangente della traiettoria formando una coppia di forze che porta al ribaltamento del proietto con il conseguente aumento di resistenza aerodinamica e perdita di precisione ed efficacia della salva.^[8] Da qui la necessità di stabilizzare i proietti imprimendo loro una veloce rotazione ottenuta mediante la rigatura elicoidale della canna che agisce sugli anelli di forzamento in metallo deformabile del proietto.^[9]

Le velocità di rotazione sono molto elevate, fino a 300 000 giri per minuto,^[10] causando un marcato effetto di precessione che, in caso di rotazione destrorsa, porta ad una derivazione del piano di tiro (il piano verticale contenente l'asse dell'arma) verso destra tanto maggiore quanto è la durata del volo del proietto.^[7]

Proiettile stabilizzato

Un proietto stabilizzato dalla rotazione impressagli dalla rigatura può essere approssimato come un corpo rigido sul cui baricentro ( $Cg$ ) agisce la forza di gravità, mentre le forze aerodinamiche non sono generalmente applicate al baricentro, ma sul centro di pressione ( $Cp$ ) che risulta anteriore al baricentro.^[11] Nel caso di proietti stabilizzati aerodinamicamente (grazie ad alette di coda) il centro di pressione è posteriore al baricentro e la descrizione delle forze e del moto è più complessa.^[12] Per le inevitabili imperfezioni del sistema di lancio (si veda la balistica interna) l'asse del proietto assume sempre un angolo $\delta$ con il vettore ${\vec {V}}$ della velocità,^[12] detto angolo di nutazione balistica.^[13] L'aria, come mezzo viscoso esercita una forza sul proietto in volo che si applica sul centro di pressione $Cp$ , tale forza si oppone al moto ed è rappresentata dal vettore ${\vec {F_{1}}}$ .^[11] Si possono aggiungere una coppia di forze ( ${\vec {F_{2}}}$ ed ${\vec {F_{w}}}$ ), uguali e contrarie, aventi lo stesso modulo di ${\vec {F_{1}}}$ applicate sul baricentro senza alterare l'equilibrio del proietto.^[13] Si considerino la coppia di forze ${\vec {F_{1}}}$ e ${\vec {F_{2}}}$ esse costituiscono una coppia avente momento ${\vec {M_{w}}}$ . Tale coppia si definisce coppia di rovesciamento.^[13] Le forze agenti sul proietto possono essere considerate la sola forza aerodinamica ${\vec {F_{W}}}$ , applicata al baricentro del proietto ed parallela alla direzione del moto ma di verso contrario ed una coppia applicata su di un asse passante per il baricentro ${\vec {M_{w}}}$ .^[13] La ${\vec {F_{W}}}$ può essere considerata la composizione di due forze: la ${\vec {F_{D}}}$ , avente la stessa direzione del vettore ${\vec {V}}$ detta resistenza aerodinamica o ritardatrice e la ${\vec {F_{L}}}$ detta forza portante o sostentatrice.^[14]

{\vec {F_{D}}}=-{\frac {\rho (p,T,h)}{2}}AC_{d}(B,M_{a},R_{e},\delta )v_{w}^{2}e_{t}

^[12]

Dove $\rho$ densità dell'aria, $(p,T,h)$ valori di pressione, temperatura e umidità dell'aria, $C_{d}$ coefficiente di resistenza aerodinamica, $A$ area della sezione frontale del proietto, $B$ è il coefficiente di forma del proietto, $M_{a}$ è il numero di Mach, $R_{e}$ numero di Reynolds, $\delta$ angolo di derivazione, $v_{w}$ velocità del proietto e $e_{t}$ è il versore tangente alla traiettoria.^[12] Considerati noti i parametri dell'aria $(p,T,h)$ e quelli geometrici e dinamici del proietto ( $A$ e $v_{w}$ ) la ${\vec {F_{D}}}$ è determinata dal $C_{d}$ coefficiente di resistenza aerodinamica.

La ${\vec {F_{L}}}$ può essere generalmente trascurata poiché di piccola entità relativa e poiché può assumere valori sia positivi sia negativi durante il volo del proietto.^[14]

{\vec {F_{L}}}=-{\frac {\rho (p,T,h)}{2}}AC_{L}(B,M_{a},R_{e},\delta )v_{w}^{2}e_{L}

e_{L}=-{\frac {1}{\sin \delta }}(e_{t}\times (e_{c}\times e_{t})v_{w}^{2}e_{t}

^[12]

Dove $C_{L}$ è il coefficiente di portanza, $e_{L}$ è il versore di ${\vec {F_{L}}}$ .^[12] La coppia di rovesciamento viene contrastata dall'effetto giroscopico impresso dalla rotazione del proietto lungo il suo asse.^[14] Il risultato è un moto dell'asse del proietto lungo una superficie conica, detta precessione.^[12]

Considerata l'impossibilità di una determinazione esatta della funzione resistente,^[15] per poter eseguire il tiro si fa riferimento a tavole di tiro che incrociando dati sperimentali, eseguiti a tre diverse elevazioni 15°, 25° e 35°, con metodi calcolo numerico, quali quello messo a punto da Francesco Siacci, permettono una ragionevole soluzione di tiro.^[16]

Note

^ Dizionario Treccani, su treccani.it.
^ Enciclopedia Treccani, su treccani.it.
^ ^a ^b ^c ^d ^e ^f Steele, pp. 348-382.
^ Cocco, p. 180.
^ Manuti, p. 25.
^ Lawton, p. 1244.
^ ^a ^b Manuti, p. 29.
^ ^a ^b Manuti, p. 27.
^ Manuti, p. 55.
^ Calcolo velocità rotazione di un proietto, su accurateshooter.wordpress.com.
^ ^a ^b Cocco, p. 163.
^ ^a ^b ^c ^d ^e ^f ^g How do bullets fly?, su nennstiel-ruprecht.de.
^ ^a ^b ^c ^d Cocco, p. 164.
^ ^a ^b ^c Cocco, p. 165.
^ Cocco, p. 189.
^ Cocco, p. 190.

Bibliografia

Antonio Cocco (a cura di), Complementi di artiglieria e tiro, vol. 1, Livorno, Poligrafico dell'Accademia Navale, 1960.
Guido Manuti (a cura di), Nozioni di artiglieria e tiro, vol. 1, parte 2ª, Livorno, Poligrafico dell'Accademia Navale, 1958.
Bryan Lawton, The Early History of Mechanical Engineering^{[collegamento interrotto]}, vol. 2, Technology and Change in History, Boston, Brill, 2004. Accesso condizionato via Questia.
Brett D. Steele, Muskets and Pendulums: Benjamin Robins, Leonhard Euler, and the Ballistics Revolution, in Technology and Culture, Vol. 35, No. 2, The Johns Hopkins University Press and the Society for the History of Technology, aprile 1994, pp. 348-382, DOI:10.2307/3106305. Accesso condizionato via Jstor.

Voci correlate

Altri progetti

Wikizionario contiene il lemma di dizionario «balistica»
Wikimedia Commons contiene immagini o altri file su balistica

Collegamenti esterni

Balistica interna, esterna e terminale, su earmi.it.
Balistica e traiettoria (PDF), su tiropratico.com.

Controllo di autorità	Thesaurus BNCF 49310

Portale Armi

Portale Meccanica

[TreccaniDizionario-1] Dizionario Treccani, su treccani.it.

[Treccani-2] Enciclopedia Treccani, su treccani.it.

[Steele-3] ^ ^a ^b ^c ^d ^e ^f Steele, pp. 348-382.

[4] Cocco, p. 180.

[5] Manuti, p. 25.

[6] Lawton, p. 1244.

[cita-Manuti-p29-7] Manuti, p. 29.

[cita-Manuti-p27-8] Manuti, p. 27.

[9] Manuti, p. 55.

[10] Calcolo velocità rotazione di un proietto, su accurateshooter.wordpress.com.

[cita-Cocco-p163-11] Cocco, p. 163.

[Nennstiel-12] ^ ^a ^b ^c ^d ^e ^f ^g How do bullets fly?, su nennstiel-ruprecht.de.

[cita-Cocco-p164-13] Cocco, p. 164.

[cita-Cocco-p165-14] Cocco, p. 165.

[15] Cocco, p. 189.

[16] Cocco, p. 190.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Balistica esterna

Indice

Storia

Balistica nel vuoto

Gittata orizzontale

Durata del tragitto

Angolo di alzo

Sviluppo per una gittata arbitraria `x`

Altezza raggiunta per `x`

Velocità del proietto alla distanza `x`

Derivazione

Alzo $\theta$ richiesto per colpire le coordinate (`x`,`y`)

Balistica nell'aria

Caso di un proietto non stabilizzato

Proiettile stabilizzato

Note

Bibliografia

Voci correlate

Altri progetti

Collegamenti esterni

Menu di navigazione

Balistica esterna

Storia

Balistica nel vuoto

Gittata orizzontale

Durata del tragitto

Angolo di alzo

Sviluppo per una gittata arbitraria x

Altezza raggiunta per x

Velocità del proietto alla distanza x

Derivazione

Alzo θ {\displaystyle \theta } richiesto per colpire le coordinate (x,y)

Balistica nell'aria

Caso di un proietto non stabilizzato

Proiettile stabilizzato

Note

Bibliografia

Voci correlate

Altri progetti

Collegamenti esterni

Menu di navigazione

Ricerca

Sviluppo per una gittata arbitraria `x`

Altezza raggiunta per `x`

Velocità del proietto alla distanza `x`

Alzo $\theta$ richiesto per colpire le coordinate (`x`,`y`)